Category: "R:WM Dev Blog"
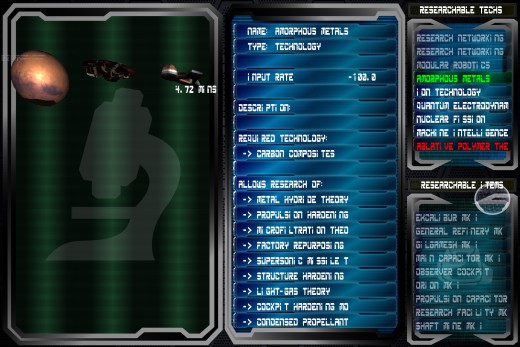
Research Screen First Look
Apr 3rd
Welcome to our new research screen. You can't conquer the solar system efficiently if you can't upgrade your equipment, so this screen will allow you to research new technology and items based off of tech you already have or based off of items you've salvaged or liberated from your rivals. One feature that I particularly like is that if you find yourself in desperate need of a particular upgrade, you'll be able to assign multiple research centers to it, driving the time to development down with each research center you add. (Up to a point, of course; there's a falloff in how much extra research each research center adds, for the sake of game balance.)

Ship progress
Apr 1st
Progress update for the ship. High poly sculpt is currently being done in Zbrush.
Full story »
Planet to Deep Space and back again
Mar 27th
A lot more work has been done on the single player, in this case, the not so well hidden navigation screen. This allows a point and click means of controlling your ships and fleet. While it has been limping along for a while, much of it's functionality required some fixing of some fundemental equations. That has now happened, so one can scroll across a planet nicely, and transition from the planet to deep space and back again. Also, the lighting finally matches the lighting in the normal simulation (for good or ill). Of course, everything is still in testing, but as always, constant improvements.

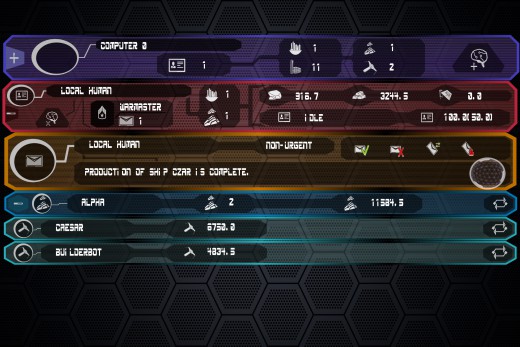
UI/UX Artist: Text Fields & Research Screen!
Mar 26th
This is your UI/UX Artist Paul and tonight I have two updates. First, I've been working on making text backdrops. Second, I've begun modernizing the Research Screen!
We've had window art for a while now, as evidenced by the variety of screenshots shown already. What we've been needing however were more "slim line" holders for situations where only individual lines of text are present, for example when loading a save file. These had to be distinguishable from their container window, and not clash with its pattern.
In this case a glassy pane look would form a nice contrast with the previously established "scanline" aesthetic, and thus ensure visibility over such a detailed background. This is somewhat important considering that text has to be legible. There are several different minor "flavor" additions that can be explored, and blue isn't a hard necessity, but for now simply having a dedicated text field is its own achievement!
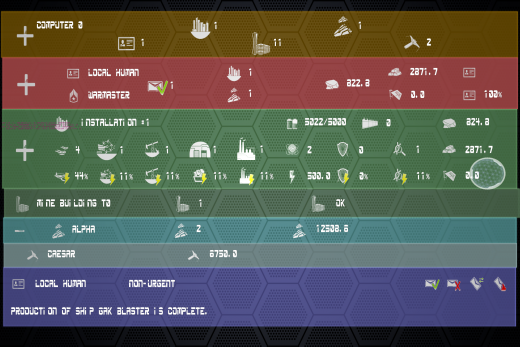
Next up was the facelift of the Research Screen. There is practicality in similarity, and so the overall layout was taken from the pre-existing Factory Screen.
For context, this is an approximation of the Factory Screen, sans minor updates.
And here we have the adapted Research Screen!
The right side window has been split into two as needed for different content; the Factory Screen held a simply vertical scroll list there, whereas this will serve other purposes. Color changes go a long way in distinguishing this screen from that the Factory. Further refinement is underway (such as the line thickness and gradient on the screen bezels), however the overall format works.
Finalized Asset Screen
Mar 23rd
In Paul's last post (UI/UX Artist: The Asset Screen Comes Together) , he showed some new asset screen art. Here's some of that same art in what's turning out to be the finalized version of the asset screen. All of the new bars are now in the game. All of the icons have tooltips, so players can see what does what on the screen. Connections between screens are currently being filled in, so you can go from a ship or a building on the asset screen directly to the Ship Builder or Building Screens.
For contrast, here's a screen shot of the original version of the asset screen. We've certainly come a long way! Next on the agenda: an updated Research Screen. Can't conquer the solar system without tech, after all!

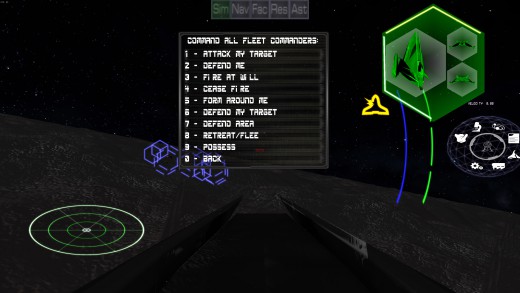
Fleet Command
Mar 15th
While a lot of behind the scenes code has been updated, the more obvious front facing code is the fleet command interface in the Sim screen. With this, this allows the player to give quick commands to their own forces, while still piloting their own ship. Even something as simple as attack my target, or Flee, it gives the player the quick ability to issue important commands. With this system in place, it actually finally completes the single player game loop, so I'm actually more comfortable calling the game in an Alpha state rather than pre-alpha. It still has a long way to go, but it's a Big milestone. A player can build their own city from scratch, research their new buildings and ship parts. They can gather resources and produce the ship designs. The final piece was being able to issue orders to those built ships to do something useful. The AI has already been able to do all of this, with the auto-save in place, one has the basic gameplay in place. The campaign engine has been functional for a while. Currently it is being used to do the tutorials which you've seen in other posts. So now to work on the Navigation screen! :)

UI/UX Artist: The Asset Screen Comes Together
Mar 11th
Hi all. This is your UI/UX Artist Paul. I'm proud to say that the Asset Screen is coming together nicely!
First is the Corporation Bar. This is more or less your "View Totals" header. This allows the player to view the overall standing of all of one's assets in one place: all personnel, installations (cities), squadrons, and ships. This bar also functions as the master dropdown for the Asset Screen, as selecting the categories will open the main bar for that item (i.e., choosing the "Installations" icon will open up the familiar-sounding the Installation Bar.)
Next we have the Personnel Bar. This bar allows the player to view their direct underlings and their pertinent information such as their Rank, Message Inbox, Current Orders, Budget, and what Resources, Cities, & Squadrons they own. This bar also gives the player control over each underling. One can grant their underling tactical advantage in the form of additional resources with the Transfer Assets icon, or "fire" them from one's employ completely via the "Delete AI" icon.
And lastly, a collection of smaller bars. Here we have the Messages Bar, the Buildings Bar, the Squadron Bar, and the Ships Bar, in descending order. The Messages Bar is a subset of the Personnel Bar, and displays in-game messages from the player's underlings. The Buildings Bar is a subset of the Installations Bar, displaying information about a certain specific building, such as a research outpost or a reactor. The Squadron Bar displays codified groups of ships, how many ships make up a given Squadron, and the total combative force that squadron presents. The Ships Bar is a subset of that Squadron Bar, displaying information about specific individual ship within that squadron.
The Warmaster Thinks You'll Enjoy This Game, And So Do I
Mar 9th
It's been a very busy couple of weeks here at LBPS Inc. Most of what I've been working on is now being tested, refined, and wrapped up. The flight sim tutorial is up and running and being tested; you can see a screenshot of that tutorial, and the Warmaster character who guides you through it, above. I have to admit I was never very good at flight sims, but I've now successfully completed this tutorial multiple times, which I was a little worried about while I was writing it. After all, how could I successfully write and test it if I can't win a simple space combat scenario? But I did win, more often than not. I guess the multiplayer test streams really paid off, and of course a lot of thanks also goes to Arthur's HUD, which makes flying these ships so much more intuitive.
The factory screen now has tool tips and a ship build timer. Small details like that, being able to tell when your ship will be complete, make quite a difference to real game play.
The asset screen continues to be greebleized, one bar at a time. (Greebles are visual details added to the otherwise plain surface of objects, in this case the bars, to make them more interesting.) This also makes a significant difference in gameplay; it's so much easier to keep track of all that data when there are visual differences to look for.

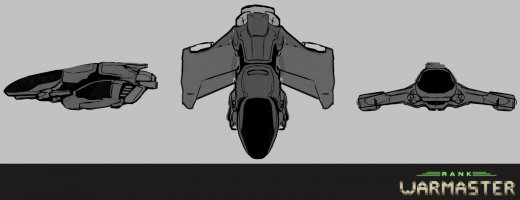
Ship Concepts
Mar 6th
New ships will soon be coming to the game. Here's a glimpse of my concept process. Some are created wtih sihouettes or pen. I'm still a bit old school and like drawing theses concepts on paper. Using pen also allows "happy mistakes" and create shapes or lines I may not have created with pencil or by tablet. Next step will be refining.